1987 The Ikeda delay differential equation
Kensuke Ikeda proposed a model of a passive optical resonator system [1]. When the system is an optical bistable resonator, Ikeda and Kenji Matsumoto showed that the dynamics can be reproduced with the single delay differential equation [2]
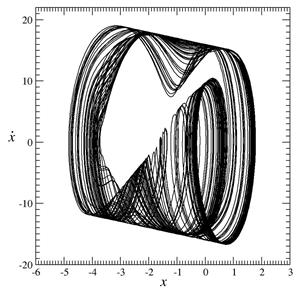
For μ = 16 and x0 = π/3, δt = 0.002 and x(0)=2.5, the chaotic attractor shown in Fig. 1 is obtained. These parameter values were obtained by looking for a simple attractor starting from those provided by Voos & Kurths [3].
- Fig. 1. A low-dimensional chaotic attractor produced by the Ikeda DDE.
[1] K. Ikeda, Multiple-valued stationary state and its instability of the transmitted light by a ring cavity system, Optics Communications, 30 (2), 257-261, 1979.
[2] K. Ikeda & K. Matsumoto, High-dimensional chaotic behavior in systems with time-delayed feedback, Physica D, 29 (1-2), 223-235, 1987.
[3] H. Voss & J. Kurths, Reconstruction of nonlinear time-delayed feedback models from optical data, Chaos, Solitons & Fractals, 10 (4–5), 805-809, 1999.