2011 A non hyperchaotic but 4D system
In 2011, Liangrui Tang, Lin Zhao, and Qin Zhang proposed a new four-dimensional system [1]
![\left\{
\begin{array}{l}
\dot{x} = a (y -x) + yz \\[0.1cm]
\dot{y} = b (x+y) - xz \\[0.1cm]
\dot{z} = cx - dz + yw \\[0.1cm]
\dot{w} = ey - fw + xz \, .
\end{array}
\right.
\left\{
\begin{array}{l}
\dot{x} = a (y -x) + yz \\[0.1cm]
\dot{y} = b (x+y) - xz \\[0.1cm]
\dot{z} = cx - dz + yw \\[0.1cm]
\dot{w} = ey - fw + xz \, .
\end{array}
\right.](local/cache-TeX/d56caf8a00b5cea679bc3301742d72ce.png)
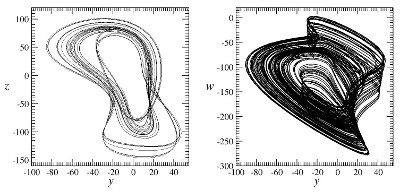
which produces an interesting attractor for the parameter values as a=55, b=25, c=40, d=13, (e=23, and f=8. Initial conditions can be as x = 0, y = 1, z = 0 and w=1. Two planes projections of the attractor are shown in Fig. 1. Contrary to what was initially claimed, this attractor is not hyperchaotic and has a single positive Lyapunov exponent [2].
- Fig. 1. Four-dimensional chaotic attractor.
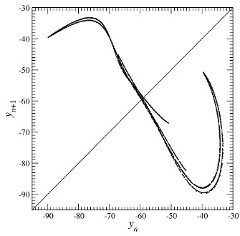
This is confirmed by the one-dimensional first-return map to a Poincaré section which is shown in Fig. 2.
- Fig. 2. First-return map to a Poincaré section.
[1] L. Tang, L. Zhao & Q. Zhang, A novel four-dimensional hyperchaotic system, In : \it Applied Informatics and Communication, Springer-Verlag, pp. 392-401, 2011.
[2] J. P. Singh & B. K. Roy, The nature of Lyapunov exponents is (+,+,-,-). Is it a hyperchaotic system ?, Chaos, Solitons & Fractals, 92, 73-85, 2016.