1972 The Malkus water wheel
As Edward Lorenz wrote himself [1] :
"The physical reality of the irregularity alternating circulation was substantiated a few years later when a versatile applied mathematicians Willem Malkus and Louis Howard, both at M.I.T. at the time, and Ruby Krishnamurti of Florida State University, temporarily abandoned their pencils and papers, and built water wheels that were specifically intended to execute the behavior predicted by the three equations, spinning clockwise for a while and then counterclockwise for a while."
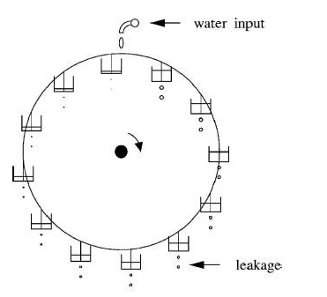
In 1972, Malkus published a first paper on this water wheel [2]. I did not find any reference by Howard and Krishnamurti. There are many papers that later investigated this water wheel. In one of them , the water wheel is depicted as shown in Fig. 1 [3] : it has 12 leaking cups hanging from its rim and filled from the top. In order to have a water wheel described by equations which are very close to the Lorenz equations, the axle of the wheel is in such a way that the main plane of the wheel is quite close to horizontal and the cups are filled by a series of water stream, symmetrically distributed with respect to the top of the wheel [4].
- Fig. 1. A water wheel made of 12 cups with a leakage. From Matson (2007).
The equations decribing such a water wheel are [3]
![\left\{
\begin{array}{l}
\dot{x} = y - f x \\[0.1cm]
\dot{y} = - \lambda y + xz \\[0.1cm]
\dot{z} = - \lambda z - xy + \lambda
\end{array}
\right.
\left\{
\begin{array}{l}
\dot{x} = y - f x \\[0.1cm]
\dot{y} = - \lambda y + xz \\[0.1cm]
\dot{z} = - \lambda z - xy + \lambda
\end{array}
\right.](local/cache-TeX/410554800ae2880341052f8d88aab047.png)
where is the angular velocity x which represents the angular velocity, y and z being coordinates of the centre of mass. This system has two parameters, ![]() which quantifies the cup leakage and f can be seen, in a first approximation, to the inverse of the time constant for the slowdown of the wheel due to axle friction and input water drag [3].
which quantifies the cup leakage and f can be seen, in a first approximation, to the inverse of the time constant for the slowdown of the wheel due to axle friction and input water drag [3].
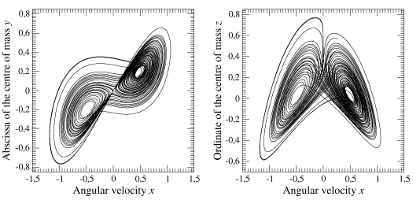
With f=0.4 and ![]() , and using the initial conditions
, and using the initial conditions
![]() , a chaotic attractor can be obtained (Fig. 2).
, a chaotic attractor can be obtained (Fig. 2).
- Fig. 2. Chaotic attractor produced by the water wheel as described by the equations proposed by Malton.
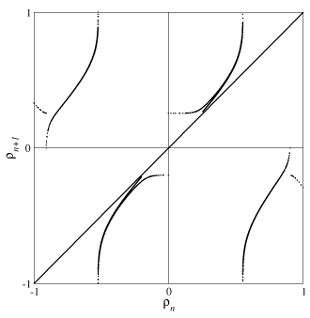
Since the chaotic attractor is bounded by a genus-3 torus, the first-return map must be computed by using a two-component Poincaré section [5]. Its structure is very similar to a first-return map to a two-component Poincaré section of the Lorenz attractor. It corresponds in fact to an attractor obtained with the Lorenz system but using a larger R-value. This chaotic attractor is therefore topologically equivalent to an attractor produced by the Lorenz system with appropriate parameter values.
- Fig. 3. First-return map to a two-component Poincaré section.
[1] E. N. Lorenz, The essence of chaos, University College London Press, 1993.
[2] W. V. R. Malkus, Non-periodic convection at high and low Prandtl number, Mémoires de la Société Royale des Sciences de Liège, IV, 125-128, 1972.
[3] L. E. Matson, The Malkus-Lorenz water wheel revisited, American Journal of Physics, 75, 1112-1122, 2007.
[4] M. Kolář & G. Gumbs, Theory for the experimental observation of chaos in a rotating waterwheel, Physical Review A, 45, 626, 1992.
[5] M. Rosalie & C. Letellier, Toward a general procedure for extracting templates from chaotic attractors bounded by high genus torus, International Journal of Bifurcation & Chaos, 24 (4), 1450045, 2014.