1984 The Chua circuit
- Leon Chua
The Chua circuit is an RLC circuit with four linear elements (two
capacitors, one resistor and one inductor) and a nonlinear diode, and
can be modeled by a system of three differential equations. The
equations for the Chua circuit are [1] :
![\left\{
\begin{array}{l}
\dot{x} = \alpha \left[ y-x-f(x) \right] \\
\dot{y} = x-y+z \\
\dot{z} = - \beta y
\end{array}
\right.
\left\{
\begin{array}{l}
\dot{x} = \alpha \left[ y-x-f(x) \right] \\
\dot{y} = x-y+z \\
\dot{z} = - \beta y
\end{array}
\right.](local/cache-TeX/5543ed3a87261c7d13b64f1bb42a01d8.png)
where

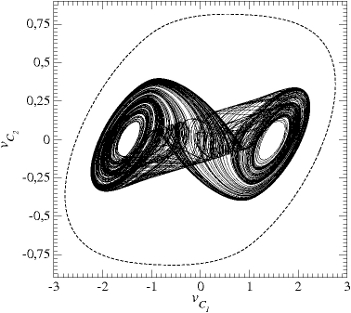
With parameter values as G=0.7, C1=1/9, C2=1, m0=-0.5, m1=-0.8, Bp=1 and L=1/7, m1=-5/7 and ![]() , a chaotic attractor is obtained (Fig. 1).
, a chaotic attractor is obtained (Fig. 1).
- Fig. 1 : Chaotic attractor solution to the Chua circuit.
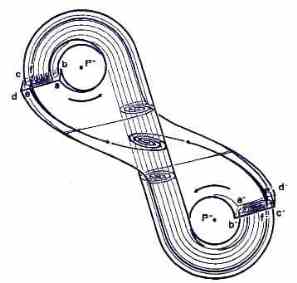
In a beautiful paper [2], the topology of this attractor was described in terms of a branch manifold (template) as shown in Fig. 2. The first electronic circuit with a five-segment odd-symmetric v-i characteristic by Farhad Ayrom (Berkeley University) and Guo-Qun Zhong (Academia Sinica, Guangzhou, People’s Republic of China), designed an electronic circuit [3]. A historical account on the discovery of this circuit is given in [4]. According to Robert Ghrist and Philip Holmes, this attractor is characterized by a template which contains all possible knots [5].
- Fig. 2 : Template for the double-scroll attractor.
[1] T. Matsumoto, A chaotic attractor from Chua’s circuit, IEEE Transactions on Circuits & Systems, 31 (12), 1055-1058, 1984.
[2] T. Matsumoto, L. O. Chua & M. Komuro, The double scroll, IEEE Transactions on Circuits & Systems, 32 (8), 798-818, 1985.
[3] G.-Q. Zhong & F. Ayrom, Experimental confirmation of chaos from Chua’s circuit, Circuit Theory and Applications, 13 (1), 93-98, 1985.
[4] C. Letellier & J.-M. Ginoux, Development of the nonlinear dynamical systems theory from radio-engineering to electronics, International Journal of Bifurcation & Chaos, 19 (7), 2131–2163, 2009.
[5] R. Ghrist & P. Holmes, An ODE whose solutions contain all knots and links, International Journal of Bifurcation & Chaos, 6 (5), 779-800, 1996.